존버력을 길러보자

평균과 분산을 억지로 외우며 듣는 여러분들께 바칩니다

(저같은 통계수업 듣는 비전공자들 화이팅...)

 평균과 분산에 대한 개념을 정말 쉽게 뿌셔보겠심당!!

우리는 이전시간에 어떠한 자료들을 대표적으로 나타내는 방법인 대표값에 대해서 배웠다

혹시라도 안보고 왔다면, 이번파트를 위한 필수적인 내용들이 있으니 마지막 부분의 요약이라도 보고오길 바란다!!

koreadatascientist.tistory.com/66

자 여기서 우리가 가장 마지막에 문제제기 한 내용을 기억하는가?

그렇다. 평균이라는 대표값 하나만으로는 해당 자료(데이터)들을 표현하기에는 역부족이란 것이다.

뜨끈한 예시

평균 점수 50점인 학생 두명의 그룹과외를 맡을 때,

평균만 보고 ok를 했다 한들,

각각의 점수가 0점과 100점이라면

골때리는 상황이 발생하기 때문....(누구에게 맞춰서 가르쳐야돼?!)

(실제 통계를 활용한 경우는 이러한 과외점수 수준의 문제들이 아니다)

오우쉣,, 그럼 저거에 대한 해결책은?!

이것에 대한 대안으로 '산포도' 의 개념이 있다. (산포도 사진이 기억나는가?)

산포도는 흩어진 정도를 의미한다. 산포도 값이 클수록 흩어진 정도가 크다.

반대로 산포도 값이 작을수록 흩어진 정도가 작을 것이다. 보통 후자(작아지는 것)를 목표로 한다. 

참고로 산포도는 음의 수가 나타나지 않는다(나중에 식을 보면 이해가 될 것)

대표값에는 6가지가 있듯이 산포도도 여러가지가 있다.

우선 가장 대표적인 산포도인 분산에 대해서 배워보자.

분산

분산의 식 형태는 이러하다. 엄밀히 이 식은 '표본'분산이다.

맨 앞단에서 기술통계학과 추론통계학이 기억나는가?

5000만명이라는 전체 집단에 대한 요약을 나타내는 통계학이 기술통계학이고

5000명을 가지고 나머지 4999만 5000명을 추론해나가는것이 추론통계학이다.

조금 더 부연설명이 필요하면 아래 링크에서 확인해보자!!

실제 세상에선 5000만명을 모두 전수조사 할 수는 없다.

대신에 5000명으로 나머지를 추론해야 한다.

이러한 과정에서 5000명을 '표본'이라고 칭하고,

해당 표본의 평균과 분산을 통해서 모집단의 평균과 분산을 추론해나가는 것이다.

지금당장 이해가 된다고 하지 않아도 문제없다.

핵심은 5000명은 표본이란 것이고, 결국 이 표본을 갖고 모집단(5000만명)을 유추해내야 한다는 것 !

이전까지는 주로 설명 위주였다면

이번에는 분산의 식에 대해서 논해야 할 필요성이 있다.

앞에서 배웠던 조화평균 기하평균과 같은 조금 더 복잡한 식은 탐구하자고 안하겠다.

대신 산포도의 대표적인 영역인 '분산'에 대한 식은 숙지해두고 있으면 앞으로의 통계 인생이 편할 것이다.

절대 쫄지 말 것. 한땀한땀 뜯어서 분해시켜보면 아무것도 아니다

자, 위의 식에서 의문을 가질수 있는 (그러나 몰랐을 때는 의문이랄게 있나 싶었던)

3가지에 대해 탐구해보자

참고로 각 통계적 기호에 대해서 초급자들은 상당히 힘들 수 있으므로, 나중에 따로 정리해둔 자료를 올릴 것이다.

그러니 여기서는 간단히만 설명하겠다.

S^2: 분산
n: 표본
x: 자기자신의 값(예: 키173, 키176, 키178, 키181 등등)
x바: 평균(예: 키의 평균 174.7)
∑(시그마): 모두 더하라

3가지에 대한 의문점

1. 왜 n이 아니라 n-1일까? (여기서 n은 표본의 수 이다 → 왜 5000명이 아니라 4999명일까?)
2. 왜 평균을 뺄까? (가장 오른쪽에 있는 x바 형태는 평균을 의미)
3. 왜 제곱을 할까? (가장 오른쪽에 자기자신인 x와 x바의 차이를 제곱한 의미)

우선 2번 3번을 먼저 논해보자. 

가장 오른쪽 식에서 제곱부분만 제외한 식을 한번 생각해보자.

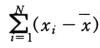
그러면 식 형태가

자기자신(x)에서 평균(x바)을 뺀것들을 모두 더하게 되는 식이 된다.

예를 들면, 키(x)가 170, 173, 176 이라고 할 때, 평균키(x바)가 173 이라면,

(170 - 173) + (173 - 173) + (176 - 173) 과 같은 형태로 되는 것이다.

충격적인 사실

그러나 어떤 데이터나 자료를 가져와도

자기자신에서 평균을 뺀 것들의 총합은 무조건 '0'이 된다.

띠용?!

위의 경우, 예시를 볼까?

-3 + 0 + 3 = 0

이것만 그럴 것 같나?

다른 예시 무한히 가져와봐라 무조건 0이다.

그래서?

이런것들은 수학적으로, 통계적으로 의미가 없다. 

다 더해서 0이 된다는게 무슨 의미가 있는데..?

그렇다면, 0이 안되도록 절댓값을 씌운다면?

|-3| + |0| + |3| = 6

(참고로 절댓값은 마이너스를 플러스로 바꾸는게 아니라 내부가 마이너스인 경우 마이너스를 붙여 나오는 것이다.)

오 다 더해도 0이 안되네?!

재밌는 사실은, 이러한 공식이 실제로 있다는 것이다!

평균절대편차

평균절대편차(mean absolute deviation)라고 한다.

좋은 산포도 중 하나이다.

생김새도 잘 보면 분산과 흡사하다.

n-1 대신 n을 쓴 것 뿐이고, 제곱 대신 절댓값을 쓴 것 뿐이다.

그런데 왜 산포도로써 표본분산은 절대값인 이 식을 채택하지 않았을까?

답은 '평균'이라는 대표값은 '제곱'과 궁합이 잘 맞기 때문이다.

?? 그게 또 뭔소리여

위에서 S^2는 표본분산의 식이다.

오른쪽 부분의 식을 보자.

x바 대신에 a라는 미지수를 넣어보자.

그렇게 하면 (x - a)^2 이 될텐데, 이것은 2차방정식의 형태로 나타낼 수 있을 것이다. 

자, 아까 산포도는 흩어진 정도를 나타내는 것이고 이는 최소가 되는것을 지향한다고 했지?

그렇다. 이 이차방정식도 최소가 되는 것을 지향하도록 설계해야되는데 (왜? 산포도는 최소가 되어야 하니까)

여기서 2차방정식의 최솟값 개념이 나오는 것이다. 

잊지 말 것 - 이 그래프에서 y값은 분산을 의미하며 이는 최소가 되어야 한다!!

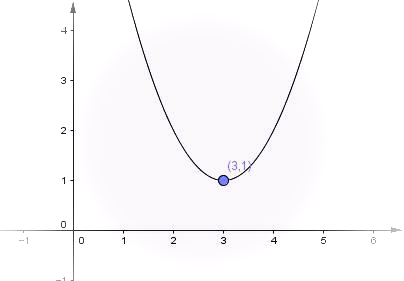
x가 3일 때에 최소값(분산이 최소가 되는 지점)이 1이 되도록 설계 하는 것이다.

만약 x가 3보다 크거나 작은 경우에는 어쨋든 y는 1보다 크기 때문에

분산이 최소가 된다고 할 수 없다. 

기억해라. 이 그래프에서 y는 산포도(분산)의 값이며 이는 최소가 되어야 한다! (누차 반복해도 모자람)

위의 식을 정의할 수 있는가? 

y = (x-3)^2 + 1 이다.

만약 최소값이 0이 되는 경우가 되려면 식이 어떠한 형태로 나와야 될까?

y = (x-3)^2 + 0 으로 나오면 되지 않을까?

👏👏👏👏👏👏👏👏👏👏

그렇다

우리가 지금까지 분산식에서 말하고자 했던 것이 이것이었다!!

y = (xi - a)^2에서 2차방정식이 최소가 되는 a값은 x바가 된다. ( 마지막에 +0이 붙은게 보이는가? )

결국 이러한 이유에서 평균을 빼버리는 제곱의 형태로 나타난다고 이해하면 된다.

절댓값의 형태인 평균절대편차의 경우는 그럼 어따가 쓰니?

여기서의 절댓값 안의 수를 최소로 만드는 x바 값은 무엇이 될까?

바로 중위수이다. 5000만명을 자산 순서대로 한 줄로 세워서 정확히 2500만명째인 사람의 위치!! 딱 중간!!

어떤 것은 산포가 최소가 되는 대표값이 평균이고(분산), 어떤 것은 중위수(평균절대편차)이고 신기하지 않은가?

나만신기한가..

자, 마지막으로 

3가지 의문점 중 첫번째인

표본분산에서 n이 아닌 n-1인 이유에 대해 알아보자.

결론적으로 한 줄로 설명할 수 있다.

"표본분산이 모분산의 불편(不偏)추정량(비편향추정량)이 되도록 하기 위해서"이다.

뭔소리야?

여기서 "불편"은 "심기가 불편하다" 가 아니라

편향되지 않은(편애하지 않다를 생각하면 쉽다)이라는 개념이다.

단계별로 생각해보자.

우선 우리가 표본을 뽑아서 추정할 때에는 '표본'은 모집단을 추정하는 일부일 뿐이다.

그렇기 때문에 표본분산과 모분산이 같을 리가 없다!!

(당연한소리, 5000명을 뽑아서 조사한 것이 실제 5000만명의 결과와 같을리는 없지않은가)

그렇지만 표본 분산은 모분산으로 향해 간다. 

표본이 많아질수록 모분산에 가까워지겠지?

여기서 모분산을 향해 가는 핵심이 n-1이다.

그래서 어쩌라는거지... n-1이 뭐냐고...

n-1은 #자유도 (degree of freedom)라고 한다.

N개의 값이 주어졌을 때의 자유도란 서로 영향을 받지 않고 독립적으로 결정되어질 수 있는 값의 개수를 뜻한다.

무적권 이해할 수 밖에 없는 예시

n=3이고 X1, X2, X3라는 임의의 값이 있다.

X에 대한 평균을 구하고자 한다.

그러면 평균은 1/3 * (X1+X2+X3) 가 되겠지?

자 여기서, 우리가 X에 대한 평균을 100이라고 가정하자.

그리고 다른 값들을 하나씩 우리가 선택해보자.

우리맘대로 X1은 50, X2는 150이라고 정해보자. 이제 X3을 정해야겠지?

근데 문제가 생겼네?

X3도 내가 마음대로 정할 수 있나?

없다

즉 여기서 X3는 다른 값에 의해 영향을 받고, 독립적으로 결정될 수 없는 값이 된다.

앞에서 본 자유도의 개념을 기억하는가?

영향을 받지 아니하고, 독립적으로 결정될 수 있는 값의 개수는 몇개인가?

방금 예에서는 설명했듯이 X1,X2로써 총 2개이다. 이게 자유도의 개념이다.

즉, 3개 중 2개가 자유롭게 결정할 수 있다는 것이다. 나머지 하나는 2개가 어떻게 되는지에 따라 바뀌니까.

마지막으로 분산과 표준편차의 관계에 대해 살펴보자

분산은 어찌됐건 제곱들의 평균이지? 

자기자신들(x)에서 평균(x바)를 뺀것들의 제곱합 형태니까!

이 제곱들의 평균(1/n-1)은 결국 기존에 우리가 궁금해했던 자료들에 비해 값이 너무 펌핑 되어서 결과가 보일 수 있다.

펌핑? 뭔소리야

키의 흩어짐(분산)을 비교하려면 평균 앞뒤로 +- 10cm 안에서 놀아야 되는데, (예를 들면 어떤 집단의 평균키가 170인데  나머지 사람들의 분포가 160~180이더라. 정도가 납득이 되잖아)

그런데 분산은 제곱들의 평균을 보여주니까 값이 10이 아닌 100이 되어버려서 해석하기에 까다롭다는 의미이다. (평균이 170인데 분산으로 표현하면 "키의 분포가 +-100cm?" → 납득이 안되고 직관적으로 이해하기도 힘든 수치이다.)

그래서 우리는 이 분산에 루트를 씌어준다. 

그러면 우리가 해석하기 용이한 10(루트100)이라는 값이 나오게 되는 것이다.

우리가 분산을 구한것은 결국 산포도를 나타내기 위함이지만,

해석의 용이성을 위해서 해당 분산 값을 루트를 씌어서 표준편차로 바꿔주는 과정이 필요하다.

분산은 계산을 위하여, 표준편차는 해석을 위하여 존재하는 것이라 이해하면 편할 것이다

조금은 쓸데 없을 수 있는 질문

그러면 애초에 분산에서 불필요하게 제곱을 하지 않고 바로 표준편차를 구하면 되잖아?!

아주 좋은 질문 !!

이미 우리가 앞에서 다룬 전제를 무시하는 질문이다.

자기자신(x)에서 평균(x바)를 뺀 것을 모두 더하면, 0이 된다. (-3 + 0 + 3 = 0 기억나는가?)

허허,, 이러한 이유로 눈물을 머금고 펌핑(제곱) 시킨 뒤에 원하는 값을 구한 후

다시 축소(루트)시키는 것이다. 그로써 표준편차가 탄생한 것이다.

핵심 요약

• 문제제기: 대표값인 평균으로는 데이터를 보여주기에 역부족
• 해결책: 분산(산포도 중 대표적인 한가지 방법)
  • 분산의 식에 대한 의문점 3가지
  • 분산에서 제곱 부분에 대한 의미
  • 분산에서 표본의수-1 (n-1)이 의미하는 것
  • 분산과 표준편차는 어떤 관계인가

해당 내용에 대해서 한줄이라도 설명이 가능하다거나, 아까 배웠던 내용이 스쳤다면 오늘 학습은 성공이다.

비전공자도 쉽게 이해하는 대표값의 개념과 산포도의 개념 뿌시기!!

대표값을 배우기 전에 이전의 내용에 대해서 충분히 숙지했는지 확인해보고 올 것!! 

우리 조직(학급이든 대학이든)에 50명의 남자가 있는데 이들의 특성을 어떻게 표현해줄까?

50명의 이름을 하나하나 나열해봤자 아무도 읽어주지 않을테고 뭔가 직관적인 것이 필요할 것 같다.

그것은 바로 단 하나의 수치!!

단 하나의 수치를 나타내줌으로써 해당 집단의 남성들의 특징을 보여줄 수 있을 것이다.

찐한 예

예를 들어 특정 조직의 남성 50명의 평균 나이가 66.7세라면 이 곳은 적어도 군대는 아닐 것이다. 

만약에 어떤 회사에서 이런 대상들을 상대로 제품을 홍보해야된다면, 아이패드가 효과적일까 도라지배즙이 효과적일까? 

적어도 전자는 아닐 것이다.

이런식으로 평균이라 함은 어떤 데이터들의 대표값으로 나타낼 수 있다.

평균이 모든 50명의 나이를 반영해주지 않지만, 이런식으로 구성되어있다는 느낌(?)은 줄 것이다.

평균은 대표값을 나타내는 방법 중 하나이다.

그 외에도 다양한 대표값이 있다.

• 산술평균
• 기하평균
• 조화평균
• 중위수
• 최빈수
• 다듬어진평균

하나하나를 일일이 외우기보다는

"아 평균으로 이렇게 다양한 경우가 있고, 평균이 아닌 애들 중에서는 중위수와 최빈수가 있구나."

정도로만 이해해보자

이 다양한 평균들의 핵심은 식 자체가 아니라!! 어떠한 상황일 때 어떤 평균의 계산법을 쓸지 정해야 된다는게 중요하다.

​

산술평균

우선 우리가 기본적으로 평균이라고 하는 것은 산술평균인데 이는 관측값을 모두 더한 값을 관측값의 수로 나누면 된다.

말이 복잡해서 그런데 50명의 학생들을 뽑아서 키를 잰 뒤에 다음과 같이 계산한다

모든 키를 더한 값 / 50명

그러면 해당 50명의 평균적인 키가 나올 것이다. 

그렇다 우리가 일반적으로 평균을 내는 방식은 산술 평균이다.

특징으로는 모든 데이터를 사용해서 어떤 계산된 값을 구하기에 적합하다는 것이다.

'모든 데이터'를 사용했다는 것이 주목할만하다.

그럼 완벽할까?

그러나 문제점이 있다.

어떤 이상치(특이한 값; outlier)가 있으면 그것에 의해 크게 좌지우지 된다는 점이다.

이상치가 평균을 망치는 예시

예를 들어 우리나라 과거에 연봉수준의 평균값이 3000~3500(만원)이라고 발표했다고 가정해보자.

그러면 어떤 사람은 내가 3300만원 이니까 우리나라 연봉의 50%(중간)쯤에 위치할 것이다 라는 생각을 할 수 있다.

하지만 이것은 큰 착각이다. 함정에 빠진 것이다.

이런 경우에 우리나라 사람 연봉을 한줄로 쭈우우욱 세워놓고 정확히 가운데 사람을 골라서 그 사람의 연봉수준을 체크해야 된다.

이것이 중위수(중앙값)이다. 한줄로 길게 늘여 놓은 것 중에 딱 가운데!

실제로는 평균이 3500이라고 해도 중위수는 2500인 경우도 허다하다.

왜냐면 돈이 많은 사람의 쪽으로 갈수록 너무 넘사벽으로 많아지기 때문에 평균점이 그쪽으로 쏠리는 것이다.

그러나 중위수는 액수와 상관없이 사람의 머릿수만을 고려하는 것이므로 돈 많은 사람쪽으로 쏠려가지 않는다.

이렇게 중앙값과 평균의 차이가 크면 클수록 이상치가 큰 영향을 끼친다고 볼 수 있으므로 이럴 경우에는 평균보다 중위수를 채택하는게 올바르다고 볼 수 있을것이다.

​

기하평균

기하평균은 식을 외우는거보다 '변동률'의 상황에서 적용한다는 것이 중요한 개념이다!

예를 들면 물가변동률이나 인구 변동률이 있다.

1년 2년 3년 4년이라는 곳에서 변동률이 매년 r1 r2 r3배 증가했다고 치면 연평균 증가율은 이 r1 r2 r3들을 다 더해서 3으로 나눈 값이 아니다. 산술평균처럼 계산하면 안된다는 의미이다.

여기서의 r은 기하평균의 공식에 대입한 값이 맞을 것이다.

수식적으로 접근하면 오히려 이해가 안될 수 있으니 변동률은 기하평균을 써야되는구나 라고 생각만 하자!

​

조화평균

조화평균이 의미있는 경우로는 지점간의 평균 속도를 계산할 때이다.

어떤 지점을 왕복할 때의 속도가 다르다고 가정할 경우 평균속도는 둘을 더해서 2로 나누는 것이 아니다.

속도의 평균은 총이동거리에서 총걸린시간을 나누기 때문이다. 

예시

출발지부터 목적지까지 가는데에 40km/h이 걸렸고,

목적지로부터 출발지까지 돌아오는데에 60km/h이 걸렸다면,

평균속도는 50km/h가 아니다! 48km/h이다!

전체 거리를 이동하는데에 48km/h로 달려야 동일한 시간에 왕복이 가능하기 때문이다.

위 예시 이해 안됨. 그러면 아래를 보자

평균구매력에 대해 살펴보자

서울시에서 A시장에서 2개에 1만원에 파는 물건이 있다고 치자. (그러면 1개에 5000원 정도네?)

옆동네 B시장에서는 3개에 2만원에 팔고 있다. (그러면 1개에 6700원 정도네?)

여기서 서울시에서 1만원으로 살 수 있는 수박의 평균 갯수를 구할 때 위처럼 산술평균을 써도 될까?

(그러면 A에서는 2개 사고, B에서는 1.5개를 사겠군?)

답은 안된다 이다.

이 경우에도 조화평균을 써야 한다.

​

최빈값(최빈: 최고 빈도)

최빈값의 대표적인 특징은 대표값 중 질적 자료에도 적용할 수 있다는 점이다. (성별, 혈액형과 같은 명목척도)

명목척도에 대한 개념이 익숙치 않다면 반드시 아래의 학습내용을 복습하고 오자!! (금방이다!!)

혈액형 중 가장 많은 혈액형이 무엇인지 우리가 앞에서 봤던 도수분포표처럼 혈액형 범주별로 다 세서 나타내보면 누가 가장 빈도가 높은지 알 수 있을 것이다.

다듬어진 평균

평균의 문제점은 가장 큰 값과 가장 큰 값이 평균의 값을 흐트러트린다는 것인데, 이러한 단점을 보완해주는 방법이다.

예시1

300명의 국회의원 자산의 평균값을 구하려고 한다.

그런데 그 집단 중 국회의원 J씨의 자산은 1조가 넘어버린다

이럴 경우 평균은 특이한 값으로 인해 상당히 높은 값을 형성할 수 있다.

이럴 경우에 대비해 '다듬어진 평균'은 이러한 굉장히 높고 낮은 사람의 경우를 제외 시켜서

평균을 산정하는 것이다.

예시2

비슷한 예로 올림픽 경기 심사점수 평균산정을 생각해보면 된다.

가끔 올림픽 경기중에 가장 높은 점수와 가장 낮은 점수를 제외시키는 것을 볼 수 있는데,

이것이 바로 특이값을 제외시키고 나머지를 평균치로 나타내는 것이다.

이는 산술평균의 단점을 보완하기 위해서 사용된다고 생각하면 된다.

대표값을 선정하는 기준

- 명목척도의 대표값은 최빈값을 쓴다. 

- 분포가 대칭이고 이상점이 존재하지 않으면 표본평균을 사용한다.

- 위와 반대로 비대칭적인 경우(이상점이 존재)에는 중앙값을 사용하고 표본평균과 비교해본다.

- 순서척도(서열척도;ordinal scale)는 중앙값을 사용한다.

대표값들의 비교

우선 그래프를 생각해봐야겠다.

우리가 보통 도수분포표에서 상대도수 히스토그램을 그리고서

해당 값을 선으로 부드럽게 이은 것을 밀도곡선, 분포곡선 이라고 한다.

이것의 내부의 합은 1이다.

어떠한 형태의 그림이 나오든 최빈값(Mode)를 알아보기는 쉽다.

봉우리가 가장 높은 쪽을 찾으면 된다.

다음으로 중앙값(Median)은 어떻게 구할까?

아까 분포곡선의 내부면적의 합은 1이라는 말을 기억하는가?

그러면 이걸 조금 활용해서, 내부의 합을 반으로 나누는 지점을 구할 수 있을까?

그렇다. 그 지점이 바로 중앙값이 되는 지점이 된다.

마지막으로 평균은 어떻게 구할까?

평균은 균형점을 찾는 것이다.

저울을 생각했을 때, 양쪽의 무게중심이 같아야 되는 것이다.

위의 그림에서 'ㅡ' 라는 바닥에 삼각형으로 어디에 위치시켜야

양쪽이 균형이 맞출지 생각하면 쉽다.

꼬리가 긴 쪽이 질량이 많다고 생각하면 평균은 꼬리가 긴 쪽​에 가깝게 형성될 것이다.

위의 그림은 조금 이해가 안 될수도 있을 것, 본인도 조금 헷갈렸음.

꼬리가 매우 길다고 생각하는 편이 이해하기에 쉬울 것이다.

자, 여기까지 숫자를 이용한 자료의 요약으로 '대표값'을 배웠다.

그런데 어떤 데이터를 요약하기에 이러한 대표값으로 충분할까?

아니다.

(띠용?!)

대표값이 요약정보로 충분하지 않다는 증거

내가 어떤 두 학생을 과외를 맡았다.

두 학생의 평균은 50점이다.

각각의 학생을 알아봤더니 A도 50점, B도 50점이어서 평균이 50점이 나온것이다.

좋다. 두 학생은 비슷한 실력일테니 과외를 하는데 큰 문제는없을 것 같다는 생각이 든다.

자, 이제 다른 두 학생도 평균이 50점이다.

알고보니 C는 0점, D는 100점인 상태이다.

섣불리 과외를 승낙했다가는 고생길이 훤하다.

왜?

어느쪽에 맞춰서 공부를 시켜야 될지 가늠이 안된다.

이렇듯 대표값만으로는 자료의 요약을 모두 설명할 수 없다.

자 이제 대표값이 완벽하지 않다는 것을 알았다.. 어떻게 해결해야 될까?

그 전에 우리가 배웠던 것들에 대해서 아주 간단하게 살펴보고 해결책을 찾아보자!

요약정리

대표값: 어떤 데이터들의 수치를 대표해주는 값

• 산술평균: 구하고픈 대상(키, 나이, 돈)을 다 더해서 머릿수만큼 나눠줌
• 기하평균: 변동률 상황(물가 변동률, 인구 변동률)에 사용
• 조화평균: 지점 간의 평균(평균 속도, 평균 구매력)을 구할 때 사용
• 중위수: 재산 순위로 줄 세워서 가운데 사람(돈의 크기에 영향 받지 않음)
• 최빈수: 많이 count 된 계급의 도수(ex.혈액형 A형이 제일 많다)
• 다듬어진평균: 맨위와 맨아래와 같은 이상치들을 뺀 평균

대표값의 문제점

대표값으로 자료를 요약하기에는 부족하다.

어떤 자료값은 평균에 밀집해있고,

어떤 자료값은 최고점과 최저점에 밀집되어 있어서 우연찮게 평균이 가운데로 형성되었을 수도 있기 때문이다.

이러한 문제점은 대표값과 다른 개념을 하나 도입해야 된다.

바로 '산포도' 이다. 

산포도는 산에 있는 포도가 아니라...(예전 범위에서 기술가정 생각나는 사람 매우 옳은 사람)

산포도는 흩어진 정도를 나타내주는 것이다.

아래부터는 살짝 부장님개그

원래 포도는 수박이었다.

그런데 수박이 흩어져서 포도라는 알맹이로 되었던 것이다. 

이해를 돕기 위해서 헛소리좀 해봤고...(이타적인 드립 이해좀...)

즉, 흩어진 정도라는 것에 집중하자.

산포도는 흩어진 정도를 의미하며,

대표값으로는 평균이 우두머리지만,

산포도에서는 분산이 우두머리이다. 

그럼 표준편차는 뭔데? 

이렇게 말꼬리물면 끝이 없다. 다 쉽게 알려줄게!

오늘 충분히 배웠으니

해당 파트는 이어지는 내용에서 자세히 배우도록 하자!

지금 생긴 문제점을 잊지마라.
평균과 같은 대표값으로는 자료의 요약을 나타내기에 부족하다는 것이다