이전에 지도학습과 비지도학습에 대해서 배웠다.
해당 내용은 그림으로 간단하게 나타냈으므로 다음 글을 슬쩍 훑고 와보자.
머신러닝, 딥러닝 개념, 지도학습 및 비지도학습 _ 비전공자의 머신러닝 딥러닝 학습기 # 1
저는 비전공자입니다. 머신러닝, 딥러닝 도대체 무엇인지 궁금했습니다. 머신러닝, 딥러닝에 관한 뉴스는 많이 봤지만 구체적으로 어떤 개념들이 있는지, 어떻게 적용 및 활용되는지에 대해 궁
koreadatascientist.tistory.com
지도학습 알고리즘은 크게 regression과 classification이 있다.

regression
오차가 가장 적은 예측선을 잘 찾아내는 것이 목표이다.

classification
정수개의 답을 잘 맞추는 것이 목표이다.
regression이건, classification이건 모든 과정은 아래와 같이 크게 3가지 순서를 따른다.
- Hypothesis - 가설을 세운다. ex. regression에서는 특정 선이 오차를 최소화 시키도록 예측한 선일 것이다.
- Cost function - 위의 가설에 대한 오차들을 계산한다
- Gradient descent algorithm - 오차를 최소화 하기 위해 미분한다.
regression
보통은 실수의 데이터를 가지고 학습을 시킨다.

위처럼 산점도에 대한 데이터가 있을 때 해당 산점도를 잘 나타내는 하나의 선을 찾는 것이다.
보통 구부러지지 않은 선을 찾는 것이 Linear Regression이라고 한다.
목표는 좋은 선을 찾도록 학습하는 것이다.
Hypothesis
그렇다면 좋은 선이 뭔데?

선의 함수가 H(x)이고 해당 식이 Wx + b 일 경우 어떤 선이 가장 좋은가?
(함수 이름인 H는 Hypothesis의 가설선을 의미)

그럴싸한(가설) 선을 하나 그어주고,
각 점과 가장 가까운 선 사이의 거리를 계산해보자
이 거리를 linear regression에서는 error라고 하며, 우리가 학습하는 용어로는 cost라고 한다.
자 그러면 다 됐나?
아직..!
H(x) (가설 선) - y (실제 값인 점) 이라는 cost(error)를 구하면 끝인거 같지만, 사실 이 자체의 cost는 의미가 조금 구리다.
왜냐하면 음수가 될 수 있기 때문에.
그러면 절댓값을 하면 되지 않을까?
이에 대해서는 분산에 대한 개념과 비슷하게 접근할 수 있는데, 여기서 설명하기 보다 아래의 글을 한번 참고해보면 왜 절댓값보다 제곱이 나은지에 대해서 알 수 있을 것이다. (아래 내용 안에서 "3가지에 대한 의문점"을 검색해보자)
(비전공자를 위한 통계학) 평균, 분산, 표준편차의 개념, 자유도는 덤으로 !
평균과 분산을 억지로 외우며 듣는 여러분들께 바칩니다 (저같은 통계수업 듣는 비전공자들 화이팅...) 평균과 분산에 대한 개념을 정말 쉽게 뿌셔보겠심당!! 우리는 이전시간에 어떠한 자료들
koreadatascientist.tistory.com
그렇기 때문에 저 값에 제곱을 구해준다.
그 후에 그것들(차이의 제곱들)을 합한 평균을 구한다.
그 결과 cost function은 W와 b의 함수가 된다.
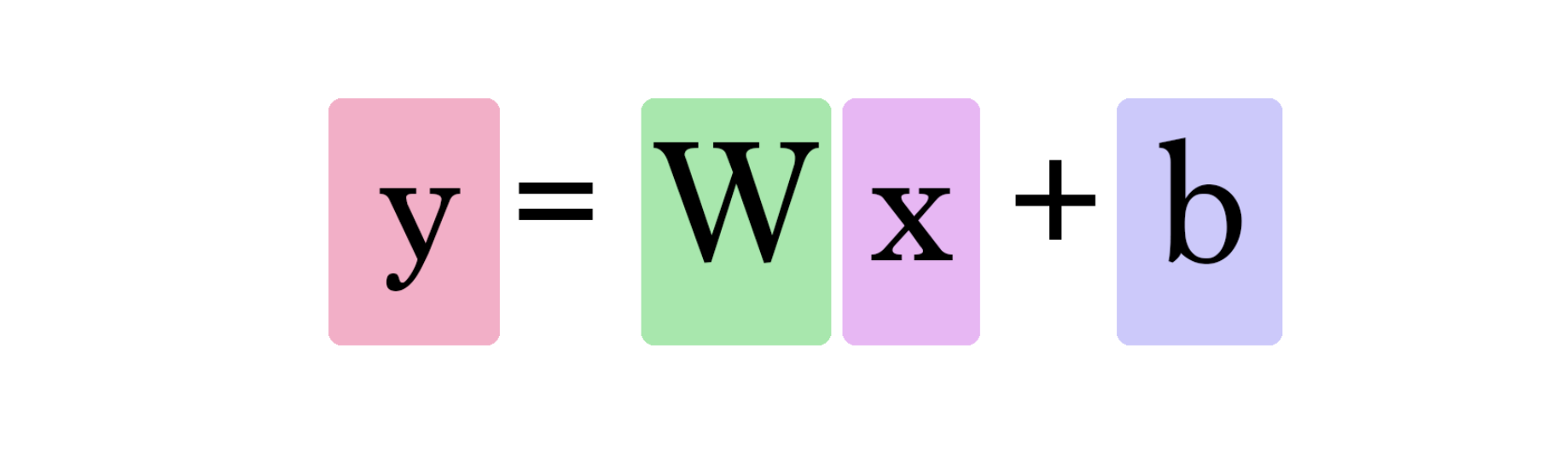
(참고로 y = ax+ b는 a와 b의 함수이다)

여기서 Y는 실제값이고, Y-hat(모자쓴모양) 은 예측값(가설 선)이 된다.
둘의 차이는 error이므로, cost라고 표현할 수 있다.
이러한 cost(W, b)를 가장 작게 하는 것이 linear regression의 학습이 된다.
그러면 cost function을 어떻게 최소화하는데?
어떻게 찾아낼까?
regression이든, classification이든 3가지의 순서를 따른다는 것을 기억하는가?
우리는 1.가설 선을 만들었고, 2.가설 선과 실제 값과의 차이(error, cost)를 구했고 이제 마지막으로 어디가 cost가 최소가 될지를 미분을 통해서 구해야 한다.
gradient descent algorithm
예를 들어 어두운 산 어딘가에서 길을 잃었다고 하자.
우리가 의존할 것은 내가 발을 디디는 곳이 아래로 가는 경사인지, 위로 가는 경사인지에만 전적으로 의존해야 한다.
이 경우에 우리는 계속 내려가는 경사만을 찾을 것이다.


이렇게 경사를 구하는 것이 순간변화율이라는 미분을 활용하는 것이고,
이 변화율이 0이 되는 지점이 cost를 최소화하는 지점이다.
(참고로 알파라는 값이 있는데 이는 보폭을 얼마나 할 것으로써, 하나의 중요한 인자가 된다)
여기서 잠깐!
convex function
W를 한 축으로, b를 한 축으로 해서 y축이 cost로 만드는 3차원 그래프를 그릴 때(아래 그래프에서 세타0 세타1이 W, b라고 생각하고 J(세타0, 세타1)이 cost라고 생각해보자)
W와 b가 각각 최소가 되는 방식으로 아래쪽으로 내려오면 하나는 동쪽, 하나는 남쪽으로 즉, 각자 다른 방향으로 내려오게 될 수도 있다. 각자 최소값이 다르게 형성된다는 것이다.

이것에 대한 해결방안으로 Convex Function을 적용하면 된다.

convex 함수는 어느 점에서 시작하든 간에, 도착하는 지점이 우리가 원하는 지점(cost가 가장 최소)을 보장한다.
동일한 산에서 3명의 사람 A, B, C어느 위치에 놔두든 산의 모양이 위와 같다면,
경사를 따라 내려가면 동일한 위치에 만나게 될테니까.
즉, cost function의 모양이 convex function이라는 것을 확인한 상태로 Gradient Descent(경사하강법; 미분)를 해야한다.

y가 cost일 때, convex가 보장되지 않은 함수라면 오른쪽 그림 중 왼쪽 점처럼 local minimum에 수렴할 수 있다.
non-convex라면, 기준이 2가지(W, b)가 되므로, 각각에 대해 낮은 2가지 cost값이 정해지는 것이다.
'파이썬 & 인공지능 > 머신러닝 & 딥러닝' 카테고리의 다른 글
| 머신러닝, 딥러닝 개념, 지도학습 및 비지도학습 _ 비전공자의 머신러닝 딥러닝 학습기 # 1 (0) | 2020.10.23 |
|---|---|
| 자연어 처리, 형태소 분석, 텍사노미, 시소러스에 대한 정리, 파이썬 형태소 분석기 mecab, kkma, komoran, hannanum, okt에 대한 결과 (0) | 2020.09.01 |